So Then, What Are
Rational Expressions
Who We Are

My notes:
1. Another, fancier, way of saying rational expressions, is ratio of two polynomials. (Keep it in your back pocket. Works against librarians.)
2. The polynomial that is present within the denominator can never have the value of 0
3. And from that we also know that any value of x that make the denominator equal to 0 are excluded
Wait, wait, what were polynomials?
a kind of number talkin’ that has parts that use letters, numbers, and whole numbers that make the letters bigger... sorry I always drool on myself when I think
a sort of math thingy that has bits that use letters, numbers, and numbers that make the letters bigger
a type of mathematical expression that consists of terms that involve variables, constants, and positive integer powers
una clase de expresión matemática que tiene partes que usan letras, números, y números que hacen las letras más grandes
4. Anytime you see Ax² + Bx + C in the denominator during these types of questions
STOP
Can I make this into an
( x +/- A )( x +/- B )
because if you can
There is a HUGE chance that you will find what you need to factor out of both the numerator and denominator. What I mean is, start here.
5. We can perform addition/subtraction/multiplication on rational expressions in order to change their denominators
We do this so that we can perform tasks such as addition and subtraction between two rational expressions that are not compared equally (eh?)
If we want to perform operation on the two fractions A/B and C/D, we have to make denominators B and D equal to each other.

YOU CANT DO THAT
In this situation, to perform the subtraction, we have use the denominator of BD. Which would give us

Beyond the A, B, C, D's .... the process just becomes proper Distribution of your numbers! Take your time.
The problem I am seeing from homework, however, is worded differently. Given an A/B, make the denominator B equal to C. While also keep A in correct value.

How do we get B = C?
For this to happen, we have to find something to multiply, D, so that
BD = C
Now we must examine the complete values for
B and C
FOR EXAMPLE NOTES
A = 2
B = X + 2
C = X² - 4
First, can we simplify into (x+/-A)(x+/-B) ??
YES
Starting with B
We can make a +4 at the end of the polynomial using -2*-2 and then we can end up with -4x by adding -2x and -2x...
Repetition
So we know then we have set B equal to
( x + 2 )
Simplifying C we have
(x + 2) * (x - 2)
So to get B equal to C, we must multiply B by (x+2)
What we do to B we will do to A as well
SO THEN THEREFORE

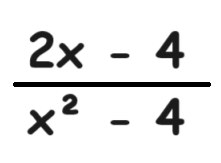
POLYNOMIAL FUNCTIONS
-
A polynomial function is a mathematical function that consists of variables raised to non-negative integer powers and multiplied by coefficients.
-
It is expressed in the form:
WHERE
are coefficients, x is the variable, and n is a non-negative integer (degree of the polynomial).
-
The highest power of the variable in a polynomial determines its degree.
Polynomial Types
-
Constant Polynomial: Degree 0, e.g., f(x)=5.
-
Linear Polynomial: Degree 1, e.g., f(x)=3x+2.
-
Quadratic Polynomial: Degree 2, e.g., f(x)=x²−4x+7.
-
Cubic Polynomial: Degree 3, e.g., f(x)=2x²+5x²−x−3.
-
Quartic Polynomial: Degree 4, e.g., f(x)=4x⁴−6x²+2x²+8x−1.
-
The roots (or zeros) of a polynomial are the values of x that make the polynomial equal to zero.
Operations We Can Perform
Operations on Polynomials:
-
Addition and Subtraction:
-
Combine like terms with the same degree.
-
-
Multiplication:
-
Multiply each term in one polynomial by each term in the other polynomial and then combine like terms.
-
-
Division:
-
Polynomial division involves dividing one polynomial by another, resulting in a quotient and possibly a remainder.
-