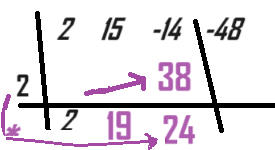
To find the factored form of the polynomial 2x³ + 15x² - 14x - 48 given that (x - 2) is a factor, you can use polynomial long division or synthetic division. Let's use synthetic division to determine the remaining factors:

 

Set up the synthetic division with (x - 2) as the divisor and the coefficients of the polynomial as the dividend:

​

​

​

​

​

Bring down the first coefficient, which is 2:

THEN

Multiply the divisor, 2, by the result from step 2 (2):

​

 

​

​

​

Add the next coefficient, 15, to the result from step 3 (4):

​

​

​

​

​

Continue the process for the remaining coefficients:

​

​

​

​

​

The numbers in the bottom row represent the coefficients of the quotient. In this case, the quotient is 2x² + 19x + 10.

​

So, the factored form of 2x³ + 15x² - 14x - 48 given that (x - 2) is a factor is:

​

(2x - 4)(x² + 19x + 10)