
Again master

This is a paragraph. I clicked in it to edit, and it's easy!
Okay, another question dealing with absolute values, but with a different equation.
Let us FIRST talk about what we know just from reading.



GPT always knows something I do not
So to continue our discussion on some narrative that communicates complex ideas dealing with a matter across time and space....
First
fine blueprint

we must do follow master
.1 For whatever value of x we will get a positive value when we calculate x - 2
.2 The value absolute value we find, will then be given a denominator of 2.
Be working on building visionary powers
.3 Ending with the addition of the positive value of 1.
Release visionary super power

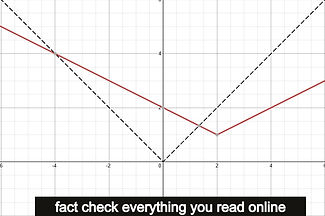
When I work on this equation, the first move I make is to zero out the value of the absolute. So, how can I make (1/2)(|x-2|) be equal to zero?
When I set the numerator to be |x-2| and then the denominator to be 2, the value of x that causes this to be 0, is:
x = 2
because
(1/2)(|2-2|)
(1/2)(|0|)
(0/2)
0
hooray x = 2 leaves
When we set x = 2 and then nullify the absolute value in a(x), we are left with the value of positive 1.
INTRODUCING
the most elegant!
refined!
BUT WHAT SO EVER DOES THIS MEAN
stout!
( 2, 1 )
get your pencil
get your paper
do your job

a lot of the work of great mathematicians is stating the obvious and sounding mysterious
VERTEX

Visualizing, we know that because of the subtraction of positive value 2 from x within the absolute brackets has shifted our vertex to the right, and then finding the zero value leaving us with 1, has our change in direction plotted at the point (2,1).
Visualizations rising, we can imagine the change in directions for our line.
For if we have negative values of x, the value of y increases
But if our value of x is positive and increasing, the value of y increases
Now the visualizations merge and we see we have an upwarding face dome of the future
Do we ever have a value of x that can cause the value of y to have a zero denominator?
NO
Domain of real numbers,