
2x³ + 15x² - 14x - 48
This equation requires us to use the rational roots theorem.
The leading coefficient of the highest power must be divisible by the denominator of the fraction AND ALSO the constant term. must be divisible by the numerator.
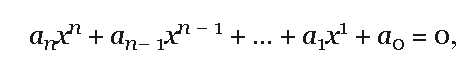
2x³ + 15x² - 14x - 48
The problem statement has given us one factor of the equation. (x-2)
So we will use that factor to begin the Ruffini's method and finish factoring the equation.

Ruffini's Method finishes to leave us with the not fully factored form of
(2x²+19x+24)(x-2)
Now focus entirely on (2x²+19x+24)
We cannot simplify 2x anymore than it already is so I know I will pull 2x out of 2x² to factor into a (2x)*(x) combination. This is just me sloppy thinking and reasoning quickly on what I can do.
Then, we also know, strictly from expreience, that we may be able to split 19x into two smaller quantities of x. We saw previously they did this so to split the equation into two parts. Remember they split the quantity of b in two numbers.
We do not know what quantities we want to split 19 into however. Let us play around and see what numbers can make good pairs for ax² and c.
So we will take bx and turn it into dx + ex. Then we can have
ax + dx + ex + c
The objective is to be able to simplify/factor
(ax + dx) + (ex + c)
separately into something simpler by themselves separately, then perhaps we can join again.
a = 2
(d + e) = 19
c = 24
Okay so here I was digging to give you an explanation better and smarter than plugging in numbers and guessing, to separate factors, but when I plug the original equation into a solver so I can see what it does, it doesnt factor out (x-2) first. It chooses (x+8). So I am back to brute force. Here is the explanation.
Solution Steps
2x³+15x²−14x−48
By Rational Root Theorem, all rational roots of a polynomial are in the form qp, where p divides the constant term −48 and q divides the leading coefficient 2. One such root is −8. Factor the polynomial by dividing it by x+8.
(x+8)(2x²−x−6)
Consider 2x²−x−6. Factor the expression by grouping. First, the expression needs to be rewritten as 2x²+ax+bx−6. To find a and b, set up a system to be solved.
a+b= −1
ab=2(−6)=−12
Since ab is negative, a and b have the opposite signs. Since a+b is negative, the negative number has greater absolute value than the positive. List all such integer pairs that give product −12.
1,−12
2,−6
3,−4
Calculate the sum for each pair.
1−12=−11
2−6=−4
3−4=−1
The solution is the pair that gives sum −1.
a=−4
b=3
Rewrite 2x²−x−6 as (2x²−4x)+(3x−6).
(2x²−4x)+(3x−6)
Factor out 2x in the first and 3 in the second group.
2x(x−2)+3(x−2)
Factor out common term x−2 by using distributive property.
(x−2)(2x+3)
Rewrite the complete factored expression.
(x−2)(2x+3)(x+8)