
First, the vertex is.
( -2, 3 )
we can view the formula to build as
f(x) = +/-(a)( | x +/- A | ) +/- B
With the vertex being (A, B)
There is a formula for plugging in the vertex and forming the graphs funtion.
Personally, I have never used it. I take the vertex numbers and jiggle them until I troubleshoot success or failure.
So, at this point. You have a -2 and a 3
Play with the +/- for plugging in those numbers
into an equation f(x) for the values B and A
and see if the values match
then you have a function!
But wait! What about the a !
This is where finding the zeros for y come in handy! We can take the vertext, and then the zero on the right side of the graph's vertex's line, and make a
f(x) = -| x + 2 | + 3
From our graph, we see that the shape is pointing downwards.
That is why we know a (-) needs to be in front of our equation.
My next step is to find the values of x for which f(x) or y equal 0
There were will two x values that satisfy the equation to equal 0
Setting
y = 0




To satisfy this, we can use either a 1 or a -5
our vertex is (-2, 3)
our zero value for y to the right of the vertex is (1, 0)
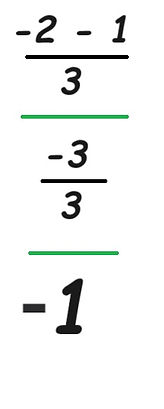
a =
Which satisfies the two points we made earlier on our graph. So our process can be confirmed correct. Our equation will satisfy the graph.