
The correct solution is at the end beginning with the picture of my dumb face.
This problem has fractions where both denominators are screaming to get factored.
I bet we factor the denominators, and then make both denominators like? I have no clue but lets start
there.
OK COMING BACK TO THIS AFTER A DAY AND
To save time, and speed the learning process.
I am going to just enter this into an AI tool, get the answer, and then build towards that answer. It can save time since it should stop me from going down the wrong path with my numbers.
AS LONG AS IN THE END YOU LEARNED SOMETHING
Learning is the only goal anyways. If you just copy/paste/fart then you did it wrong.
NEVERMIND I SEE WHERE IM GOING SCRATCH AI
Our two denominators look as if they are not going to be difficult to factor and simplify.
3x+9 and x²+3x
(3)(x+3) and (x)(x+3)
Now, to get like denominators, we will multiply the fraction on the left by (x/x) and then multiply the fraction on the right by (3/3)
Which gives us
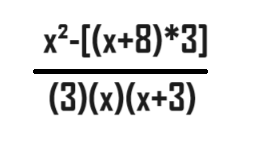
Which is super ugly so I did go put it in GPT
THEN THIS IS GPT FIRST MOVE


But.. I did that too...
...then next it went...

...and next to combine like denominators...

DISTRIBUTION OF NEGATIVE SIGN
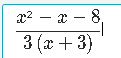
...because it didnt do that previously when combining.
ENDING WITH THE REPEAT OF

I DONT TRUST IT JUST BECAUSE IM TOLD TO
SO LETS PICK BACK UP IN THE HUMAN ADVENTURE!!
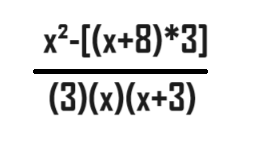
I am going to distribute it out fully and look at it.

So then I start having more than one idea on where to go, and decide to let GPT think about it
GPT wants us to factor the denominator like we have had it previously at
3x²+9 == 3(x²+3)
Then we use factors (x-6)(x+4) to separate out the numerator.
BRINGING US TO


YOU MUST WATCH GPT MATH
BECAUSE WE HAD GOTTEN A DIFFERENT ANSWER


We are both the same except the coeffecient of x in the numerator.
SOMEBODY DID WRONG
I will come back later. Try to get more done first.

START OVER
Start by finding the common denominator

In this problem the most common I can conjure is just simply puttin both of them together.
Rewritten below.

Once you have them like denominators, we will combine them together into their subtraction operation.


-
Once we have all the values together over the same denominator we can begin simplifying.
First, take the numerator value for the fraction on the left side and distribute the variable x with degree power 1 to inside the adjacent enclosed parethesis.

Now take the second fraction on the right side of our equation and we will apply the Distributive property in order to form more simpler value.
After using our Distributive property, we can combine like terms to result in the following
We can be satisfied with our two values of numerator now, and place them both back onto their respective denominators.
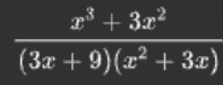
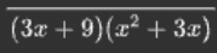
-
Now we can place both fraction's numerators above the same denominator and perform operations


